We study vortex dynamics in experiment using vortices in fluids as a model system. A recent advance [1] allows us to create vortices of controlled shape and topology which we image using a scanning tomography setup in three dimensions at high speed (~10 GVoxels/second). Open questions include the role of vortex reconnections in dissipative flows, the extent of topological conservation laws in real fluids and general aspects of vortex dynamics.
[1] W.T.M. Irvine and Dustin Kleckner, Nature Physics DOI: 10.1038/NPHYS25601745-2481 (2013).
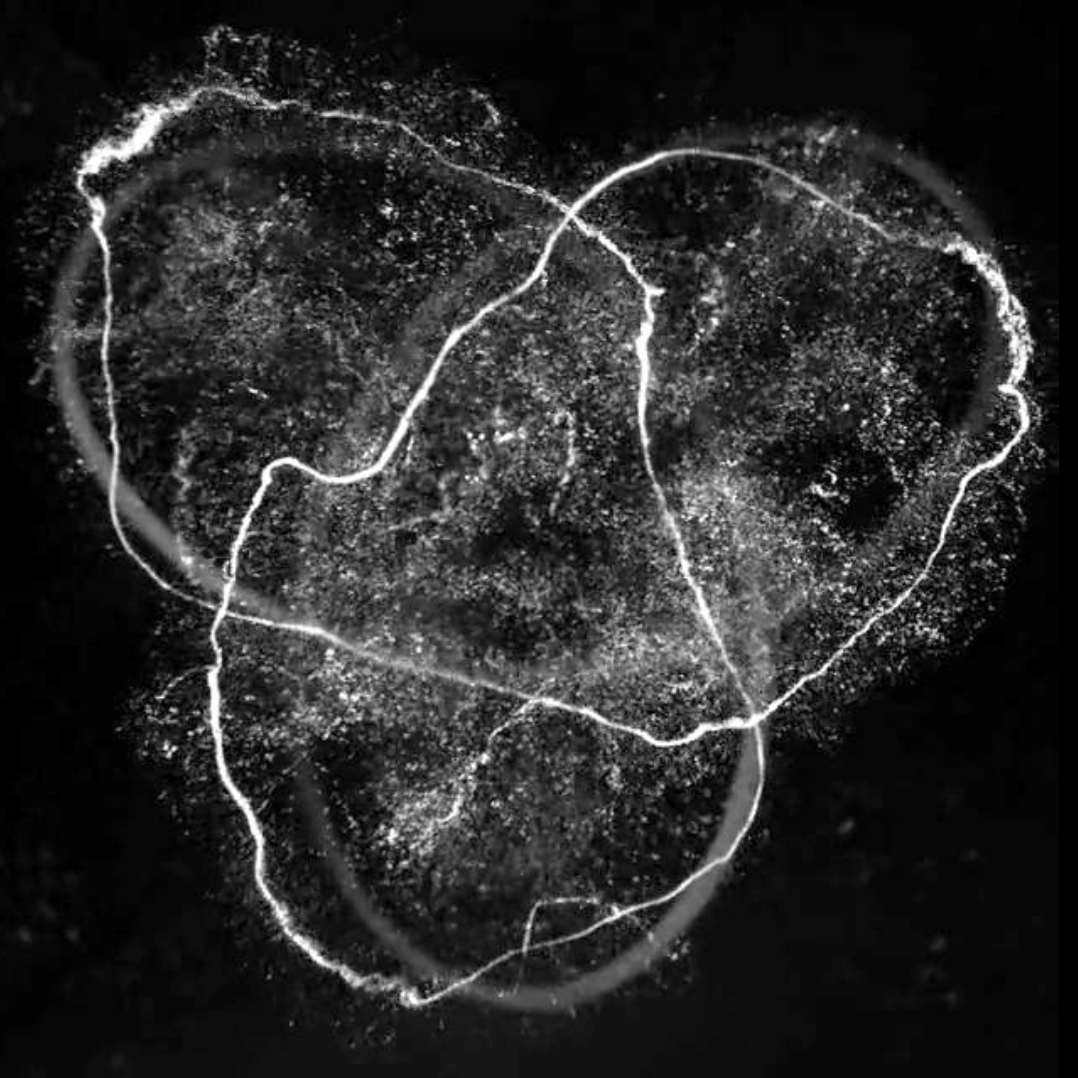
While tying a shoelace into a knot is a relatively simple affair,
tying a field, for example a magnetic field, into a knot is a different
story: the entire space-filling field must be twisted everywhere to
match the knot being tied at the core.
This interplay between knots and and the space they live in lies at the
heart of modern topology; beyond the world of mathematics, there is a
growing realization that knots in space-filling fields are an essential
part of physical processes spanning classical and quantum field theories,
liquid crystals, electromagnetism, plasmas, and quantum and classical fluids.
Linked and knotted structures in free space electromagnetic fields provide
an opportunity to study a nontrivial topological structure in the setting
of a linear field theory as well ad a means of potentially transferring
knottedness to matter [1], [2], [3].
Taking this as a starting point we are elucidating the 'rules' for
the mathematical construction and dynamical
evolution of knotted fields in general.
[2] W.T.M. Irvine, Journal of Physics A: Mathematical and Theoretical 43, 385203 (2010).
[3] H. Kedi et al., Submitted for publication.
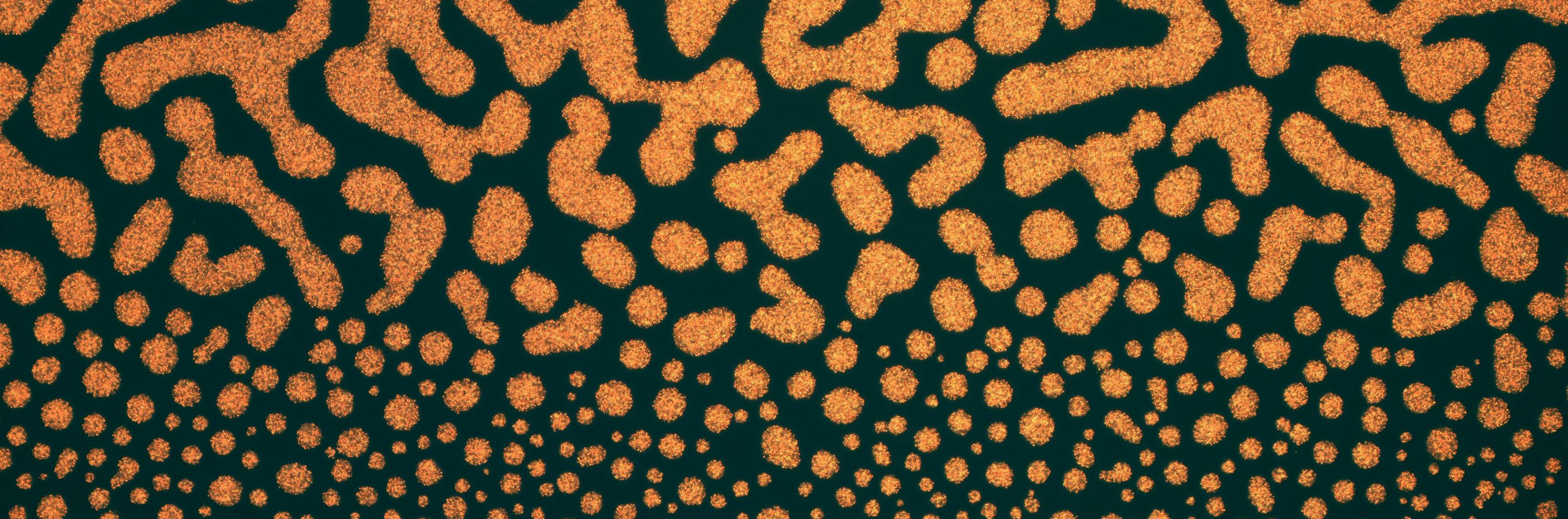
We study open questions in equilibrium and non-equilibrium many-body physics, often with an emphasis on problems in which geometry and topology provide the key to understanding the physical phenomena we observe.
Using colloidal particles, (both spherical and shaped), fluids and foams, we study the self-assembly and properties of ordered and disordered phases, while developing methods to control them. Examples include studying the interaction of topological defects with curved space [1], defect dynamics [2] and and the packing of `superballs' [3],
[1] W.T.M. Irvine et al., Nature 468 , 947-951 (2010).
[2] W.T.M. Irvine et al., Nature Materials 11, 948-951 (2012).
[3] L. Rossi et al., (In preparation)
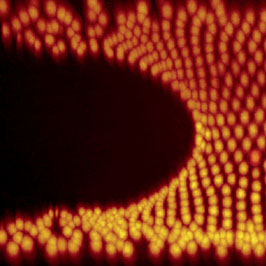
In collaboration with Efi Efrati,
we are studying phenomena that exhibit chiral behavior and developing conceptual
frameworks for their quantification, leading to improved designs for chiral materials.
See our recent manuscript [1] for more details.
[1] E. Efrati and W.T.M. Irvine, submitted (2012).
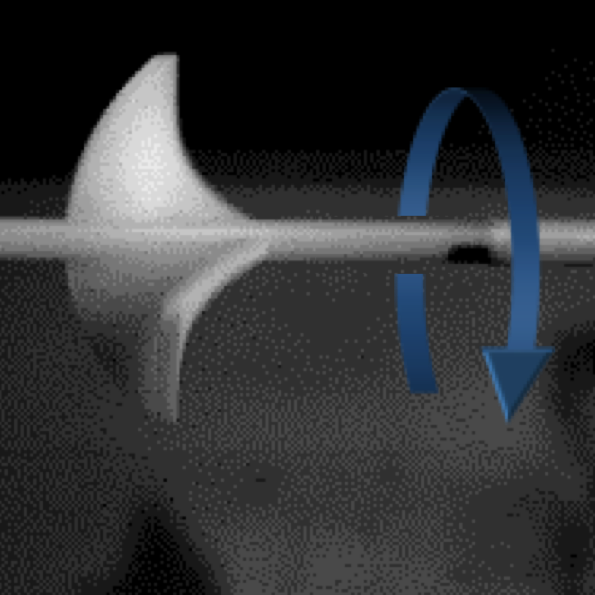
We are developing model systems to control and investigate the physics of material fracture and shock propagation. Watch this spot for more to come...
